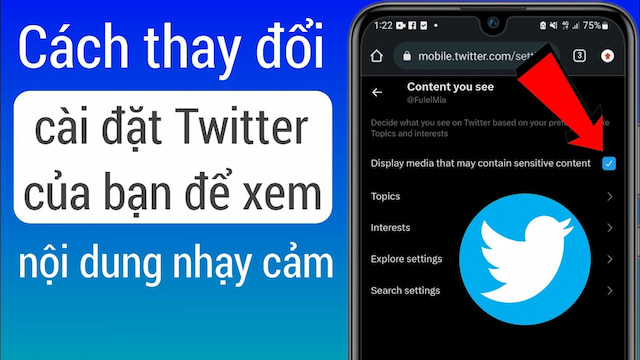
Twitter là một nền tảng mạng xã hội cho phép người dùng chia sẻ các tin tức, ý kiến, câu chuyện ngắn dưới dạng các tweet. Để sử dụng Twitter một cách hiệu quả và an toàn, bạn cần biết cách thay đổi cài đặt của ... Xem chi tiết
Main Content
Mạng xã hội
Cách Thay Đổi Cài Đặt Twitter Một Cách Nhanh Chóng
Cách Mở Chặn Telegram Siêu Đơn Giản & Nhanh Chóng
Ứng dụng nhắn tin miễn phí Telegram với độ bảo mật cao và tiện lợi cho người dùng. Tuy nhiên, nếu bạn gửi tin nhắn quá nhiều thì đôi khi tài khoản Telegram sẽ bị chặn. Cách giải quyết cụ thể vấn đề cách mở chặn ... Xem chi tiết
Thủ thuật

Cách Thay Đổi Cài Đặt Twitter Một Cách Nhanh Chóng
Twitter là một nền tảng mạng xã hội cho phép người dùng chia sẻ các tin tức, ý kiến, câu chuyện ngắn dưới dạng các tweet. Để sử dụng Twitter một cách hiệu quả và an toàn, bạn cần biết cách thay đổi cài đặt của ... Xem chi tiết

Cách Mở Chặn Telegram Siêu Đơn Giản & Nhanh Chóng
Ứng dụng nhắn tin miễn phí Telegram với độ bảo mật cao và tiện lợi cho người dùng. Tuy nhiên, nếu bạn gửi tin nhắn quá nhiều thì đôi khi tài khoản Telegram sẽ bị chặn. Cách giải quyết cụ thể vấn đề cách mở chặn ... Xem chi tiết
Bài viết mới nhất
Cách Thay Đổi Cài Đặt Twitter Một Cách Nhanh Chóng
Twitter là một nền tảng mạng xã hội cho phép người dùng chia sẻ các tin tức, ý kiến, câu chuyện ngắn dưới dạng các tweet. Để sử dụng Twitter một cách hiệu quả và an toàn, bạn cần biết cách thay đổi cài đặt của ... Xem chi tiết
Cách Mở Chặn Telegram Siêu Đơn Giản & Nhanh Chóng
Ứng dụng nhắn tin miễn phí Telegram với độ bảo mật cao và tiện lợi cho người dùng. Tuy nhiên, nếu bạn gửi tin nhắn quá nhiều thì đôi khi tài khoản Telegram sẽ bị chặn. Cách giải quyết cụ thể vấn đề cách mở chặn ... Xem chi tiết